Note
Go to the end to download the full example code.
Estimate Net AEP and P90 AEP#
Example of estimating the Net AEP and P90 AEP using a loss table and an uncertainty table. For a more detailed overview see PyWAsP Tutorial 6.
We part from the fact that user has already calculated the Potential AEP and the Gross AEP.
import pywasp as pw
import windkit as wk
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
from scipy.stats import norm
from pathlib import Path
data_dir = Path("../../../modules/examples/tutorial_1/data/")
gross_aep = xr.open_dataset(data_dir / "aep_nowake.nc")
potential_aep = xr.open_dataset(data_dir / "aep_park2.nc")
wtg = wk.read_wtg(data_dir / "Bonus_1_MW.wtg")
/home/neil/DTU/repos/pywasp/modules/windkit/windkit/wind_farm/wind_turbine_generator.py:388: FutureWarning: In a future version of xarray the default value for data_vars will change from data_vars='all' to data_vars=None. This is likely to lead to different results when multiple datasets have matching variables with overlapping values. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set data_vars explicitly.
merged = xr.concat(datasets, dim="mode")
Losses towards P50 - Importing a loss table#
loss_table = wk.get_loss_table("dtu_default")
# Modify loss values as needed
loss_table.loc[0, "loss_percentage"] = 0.5
loss_table.loc[2, "loss_percentage"] = 0.1
print(loss_table.head())
loss_name loss_percentage loss_category loss_lower_bound loss_upper_bound loss_default description
0 turbine_availability 0.5 Availability 0 5 1.0 Turbine availability losses, including downtim...
1 balance_plant_availability 0.0 Availability 0 5 0.0 Balance of plant availability losses, includin...
2 grid_availability 0.1 Availability 0 5 0.5 Grid availability losses, excluding curtailmen...
3 electrical_operation 0.5 Electrical 0 5 0.5 Electrical losses, including transformer and c...
4 wf_consumption 0.2 Electrical 0 5 0.2 Wind farm consumption losses, including auxili...
Losses towards P50 - Calculating the Net AEP#
net_aep = pw.net_aep(loss_table, potential_aep)
print("Net AEP:", net_aep["net_aep"].values.sum(), "GWh")
Net AEP: 39.19268893208979 GWh
Uncertainties towards P90 - Importing a uncertainty table#
uncertainty_table = wk.get_uncertainty_table()
print(uncertainty_table.head())
print(uncertainty_table.tail())
uncertainty_kind uncertainty_name uncertainty_percentage uncertainty_category uncertainty_lower_bound uncertainty_upper_bound uncertainty_default description
0 wind representativeness_long_term_period 2.0 Historical_wind_resource 0 5 2.0 Uncertainty associated with the statistical re...
1 wind reference_data_consistency 0.5 Historical_wind_resource 0 5 0.5 Uncertainty associated with the accuracy or re...
2 wind long_term_adjustment_mcp 1.5 Historical_wind_resource 0 5 1.5 Uncertainty associated with the MCP process, i...
3 wind ws_distribution_uncertainty 0.5 Historical_wind_resource 0 5 0.5 Uncertainty associated with the representative...
4 wind on_site_data_synthesis 0.2 Historical_wind_resource 0 5 0.2 Uncertainty associated with gap-filling missin...
uncertainty_kind uncertainty_name uncertainty_percentage uncertainty_category uncertainty_lower_bound uncertainty_upper_bound uncertainty_default description
29 energy exposure_changes 0.00 Environmental 0 5 0.00 Uncertainty associated with exposure changes l...
30 energy load_curtailment 0.01 Curtailments 0 5 0.01 Uncertainty associated with load curtailment l...
31 energy grid_curtailment 0.00 Curtailments 0 5 0.00 Uncertainty associated with grid curtailment l...
32 energy environmental_curtailment 0.01 Curtailments 0 5 0.01 Uncertainty associated with environmental curt...
33 energy operational_strategies 0.01 Operational_strategies 0 5 0.01 Uncertainty associated with operational strate...
Note
Terms that are part of the “energy” kind are those related to the uncertainties of the technical losses. Terms that are part of the “wind” kind are those related to the uncertainties of the predicted wind climate.
Uncertainties towards P90 - Calculating the Px yield#
Note
For a P90 value, x = 90.
p90 = pw.px_aep(uncertainty_table, net_aep, sensitivity_factor=1.5, percentile=90)
print("The P90 is:", p90["P_90_aep"].values.sum(), "Gwh")
The P90 is: 34.81814675313252 Gwh
tot_sigma, _, _ = wk.total_uncertainty(uncertainty_table, 1.5)
p50 = np.round(net_aep["net_aep"].values.sum(), 2)
sigma_tot_dimensional = np.round(tot_sigma / 100 * p50, 2)
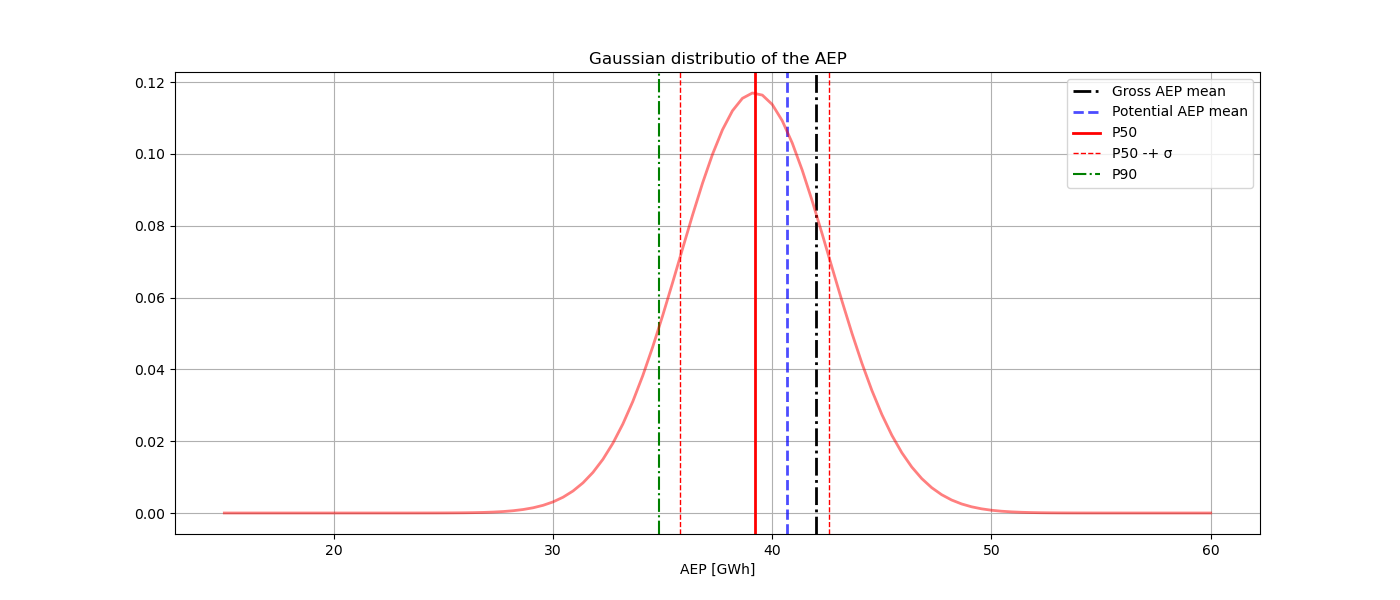
plt.figure(figsize=(14, 6))
x = np.linspace(15, 60, 100)
plt.axvline(
gross_aep["gross_aep"].values.sum(),
color="k",
linestyle="-.",
linewidth=2,
label="Gross AEP mean",
)
plt.axvline(
potential_aep["potential_aep"].values.sum(),
color="b",
linestyle="--",
alpha=0.7,
linewidth=2,
label="Potential AEP mean",
)
plt.axvline(p50, color="r", linestyle="solid", linewidth=2, label="P50")
plt.axvline(
p50 + sigma_tot_dimensional,
color="r",
linestyle="dashed",
linewidth=1,
label="P50 -+ σ",
)
plt.axvline(p50 - sigma_tot_dimensional, color="r", linestyle="dashed", linewidth=1)
plt.axvline(
p90["P_90_aep"].values.sum(), color="g", linestyle="-.", linewidth=1.5, label="P90"
)
pdf = norm.pdf(x, p50, sigma_tot_dimensional)
plt.plot(x, pdf, color="r", linewidth=2, alpha=0.5)
plt.grid(True)
plt.legend()
plt.title("Gaussian distributio of the AEP")
plt.xlabel("AEP [GWh]")
Text(0.5, 36.72222222222221, 'AEP [GWh]')
Total running time of the script: (0 minutes 0.159 seconds)

